오차역전파법(Backpropagation)
기울기 계산을 효율적이고, 고속으로 수행하는 기법입니다.
오차역전파법을 쓰면 수치 미분을 사용할 때와 거의 같은 결과를 훨씬 빠르게 얻을 수 있다는 장점이 존재합니다.
신경망 학습은 시간이 오래 걸리니, 시간을 절약하려면 오차역전파법 사용하는 것이 좋습니다!
말 그대로 오차역전파법은 순전파의 반대로 간다고 생각하시면 됩니다.
본 글에서는 수식이 아닌 계산 그래프를 통해 오차역전파법을 설명하겠습니다.
계산 그래프(computational graph)
계산 과정을 그래프로 나타낸 것입니다.
복수의 노드(node)와 에지(edge)로 표현합니다.
- 노드 : 원으로 표현하고 원 안에 연산 내용 적음
- 에지 : 노드 사이의 직선
계산 그래프의 특징은 국소적 계산을 전파함으로써 최종 결과를 얻는다는 점입니다.
- 국소적 계산 : 전체에서 어떤 일이 벌어지든 상관없이 자신과 관계된 정보만으로 결과를 출력
각 노드는 자신과 관련한 계산 외에는 아무것도 신경 쓸 게 없습니다.
전체 계산이 아무리 복잡하더라도 각 단계에서 하는 일은 해당 노드의 국소적 계산밖에 없습니다.
계산 그래프의 이점
- 국소적 계산
- 전체가 아무리 복잡해도 각 노드에서 단순한 계산에 집중하여 문제를 단순화할 수 있음
- 중간 계산 결과를 모두 보관할 수 있음
- 역전파를 통해 ‘미분’을 효율적으로 계산할 수 있는 점
순전파 & 역전파
순전파(forward propagation) :
- 계산을 왼쪽에서 오른쪽으로 진행하는 단계
- 계산 그래프의 출발점부터 종착점으로의 전파
역전파(backward propagation) :
- 순전파 반대 방향
- 오른쪽에서 왼쪽의 전파

연쇄 법칙(chain rule)
역전파는 ‘국소적인 미분’을 순방향과는 반대인 오른쪽에서 왼쪽으로 전달합니다.
국소적 미분을 전달하는 원리가 연쇄 법칙에 따른 것입니다.
계산 그래프의 역전파
- 순방향과는 반대 방향으로 국소적 미분을 곱한다.
- 신호 E에 노드의 국소적 미분을 곱한 후 다음 노드로 전달
- 국소적 미분 : 순전파 때의 y=f(x) 계산의 미분을 구한다는 뜻

연쇄 법칙은 합성 함수의 미분에 대한 성질이며, 다음과 같이 정의됩니다.
- 합성 함수의 미분은 합성 함수를 구성하는 각 함수의 미분의 곱으로 나타낼 수 있다.
- 역전파가 하는 일은 연쇄 법칙의 원리와 같다.
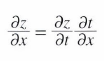
덧셈 노드, 곱셈 노드의 역전파
덧셈 노드의 역전파

왼쪽 : 순전파, 오른쪽 : 역전파
덧셈 노드의 역전파는 입력 값을 그대로 흘려보냅니다.
곱셈 노드의 역전파

왼쪽 : 순전파, 오른쪽 : 역전파
곱셈 노드 역전파는 상류의 값에 순전파 때의 입력 신호들을 ‘서로 바꾼 값’을 곱해서 하류로 보냅니다.
덧셈의 역전파에서는 상류의 값을 그댈 흘려보내서 순방향 입력 신호의 값은 필요하지 않았지만, 곱셈의 역전파는 순방향 입력 신호의 값이 필요합니다.
그래서 곱셈 노드를 구현할 때는 순전파의 입력 신호를 변수에 저장해둡니다.
활성화 함수 계층 구현 (ReLU, Sigmoid)
ReLU 계층



- 순전파 때의 입력인 x가 0보다 크면 역전파는 상류의 값을 그대로 하류로 흘림
- 반면, 순전파 때 x가 0 이하면 역전파 때는 하류로 신호를 보내지 않음 (0을 보냄)
Sigmoid 계층
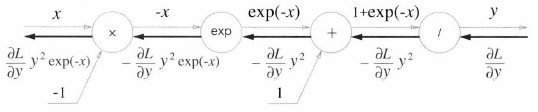
- 순전파의 입력 x와 출력 y 만으로 계산할 수 있음
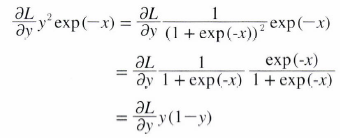
다음과 같이 정리하게 되면 sigmoid 계층의 역전파는 순전파의 출력(y)만으로 계산할 수 있음을 알 수 있습니다.
Affine / Softmax 계층 구현
Affine 계층
신경망의 순전파 때 수행하는 행렬의 곱은 기하학에서는 어파인 변환 (Affine transformation)이라고 합니다.
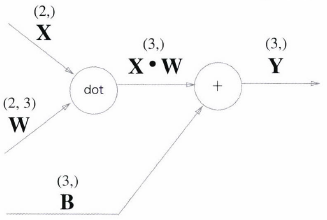
- X, W, B가 행렬(다차원 배열)이라는 점에 주의
- 지금까지의 계산 그래프는 노드 사이에 스칼라 값이 흘렀는 데 반해, Affine 계층은 행렬이 흐르고 있음
Affine 계층의 역전파는 다음과 같습니다.
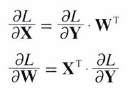
- T : 전치 행렬 의미
- 증명 과정은 복잡하여 생략하겠습니다.
배치용 Affine 계층
지금까지 설명한 Affine 계층은 입력 데이터로 X 하나만을 고려했습니다.
데이터 N개를 묶어 순전파하는 경우, 즉 배치용 Affine 계층을 생각해봅시다.
묶은 데이터를 ‘배치’라고 부릅니다.
- 기존과 다른 부분은 입력인 X의 형상이 (N,2)가 된 것뿐
- 편향의 역전파는 그 N개의 데이터에 대한 미분을 데이터마다 더해서 구함
Softmax 계층
출력층에서 사용하는 소프트 맥스 함수에 관한 설명입니다.
소프트맥스 함수는 입력 값을 정규화하여 출력합니다.
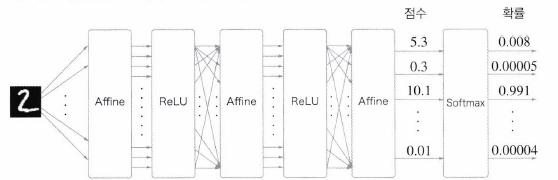
신경망에서 수행하는 작업은 '학습'과 '추론' 두 가지입니다.
- 추론할 때는 일반적으로 Softmax 계층을 사용하지 않음
- 추론할 때는 마지막 Affine 계층의 출력을 인식 결과로 이용
- 또한, 신경망에서 정규화하지 않는 출력 결과( Softmax 앞의 Affine 계층의 출력)를 점수(score)라고 함
- 즉, 신경망 추론에서 답을 하나만 내는 경우에는 가장 높은 점수만 알면 되니 Softmax 계층은 필요 없다는 것
- 반면, 신경망을 학습할 때는 Softmax 계층 필요
손실 함수인 교차 엔트로피 오차도 포함하여 ‘Softmax-with-Loss 계층’이라는 이름으로 구현해보겠습니다.
softmax-with-Loss 계층은 다소 복잡합니다.
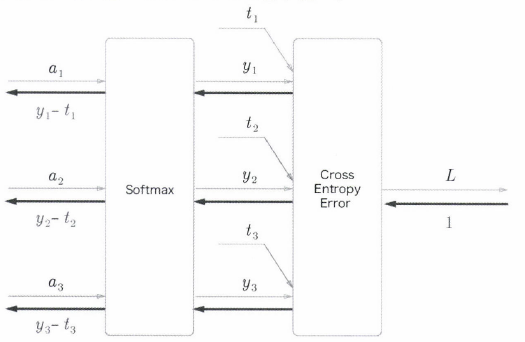
Softmax 계층의 역전파 : (yk - tk)
- yk : Softmax 계층의 출력
- tk : 정답 레이블
- Softmax 계층의 출력과 정답 레이블의 차분
- 신경망의 역전파에서는 이 차이인 오차가 앞 계층에 전해짐
- 신경망 학습의 중요한 성질!
- ‘소프트맥스 함수’의 손실 함수로 ‘교차 엔트로피 오차’를 사용하니 역전파가 말끔히 떨어짐
- 이런 말끔함은 우연이 아니라 교차 엔트로피 오차라는 함수가 그렇게 설계되었기 때문
- 회귀의 출력층에서 사용하는 ‘항등 함수’의 손실 함수로 ‘오차제곱합’을 이용하는 이유도 이와 같음
- 즉, ‘항등 함수’의 손실 함수로 ‘오차제곱합’을 사용하면 역전파의 결과가 (yk - tk)로 말끔히 떨어짐
정리 : 신경망 학습의 절차
전제
- 신경망에는 적응 가능한 가중치와 편향이 있고, 이 가중치와 편향을 훈련 데이터에 적응하도록 조정하는 과정을 ‘학습’이라고 함.
- 미니배치
- 훈련 데이터 중 일부를 무작위로 가져옴
- 이렇게 선별한 데이터를 미니배치라 하며, 그 미니배치의 손실 함숫값을 줄이는 것이 목표
- 기울기 산출
- 미니배치의 손실 함수 값을 줄이기 위해 각 가중치 매개변수의 기울기를 구함
- 기울기는 손실 함수의 값을 가장 작게 하는 방향을 제시
- 매개변수 갱신
- 가중치 매개변수를 기울기 방향으로 아주 조금 갱신
- 반복
오차역전파법은 두 번째 단계인 ‘기울기 산출’에서 등장합니다.
원래는 기울기를 구하기 위해서 수치 미분 사용하였지만, 수치 미분은 구현하기는 쉽지만 계산이 오래 걸렸습니다.
오차역전파법을 이용하면 느린 수치 미분과 달리 기울기를 효율적이고 빠르게 구할 수 있습니다.
Reference
본 글은 '밑바닥부터 시작하는 딥러닝'을 참고하여 작성하였습니다.
'Data Science > Deep Learning' 카테고리의 다른 글
| [DL] 배치 정규화(Batch Normalization), 가중치 감소(weight decay), 드롭아웃(Dropout) (0) | 2022.03.17 |
|---|---|
| [DL] 신경망 학습 - 매개변수 갱신, 가중치의 초기값 (0) | 2022.03.17 |
| [DL] 신경망 학습 (0) | 2022.03.04 |
| [DL] 손실함수 (Loss Function) : 오차제곱합(SSE), 교차 엔트로피 오차(Cross-Entropy) (0) | 2022.03.04 |
| [DL] 신경망(Neural network) (0) | 2022.02.25 |




댓글