[Paper Review] N-BEATS

N-BEATS (Neural basis expansion analysis for interpretable time series forecasting)

지금까지 대회에서 1등을 하던 모델은 항상 통계기반 모델이었지만 M4 Competition에서 우승을 차지한 모델은 ES-RNN(Exponential Smoothing Long Short Term Memory networks) 으로 통계적 방법론과 머신러닝 방법론을 잘 섞은 구조의 모델입니다.

 

그런데 그 ES-RNN보다 더 좋은 예측 성능을 보이는 순수 머신러닝 방법론이 등장했고,

그게 바로 N-BEATS or NBEATS 라고 불리는 단변량 예측 모델입니다.

N-Beats는 Time Series(시계열 데이터)를 처리하기 위해 end-to-end deep learning approach를 시도했습니다.

 

이 논문의 2가지 부분에서 기여점이 있습니다.

• 딥러닝 아키텍처
  • 통계적 접근법을 전혀 사용하지 않고 시계열 문제(Time-Series)에서 뛰어난 성과를 보인 딥러닝 아키텍처를 제시
  • 순수한 ML/DL만으로 시계열 데이터에서 효과를 낼 수 있음을 보이고 싶음
• 해석이 가능한 구조
  • “계절적 트렌드” 와 같은 특징들을 분석할 수 있는 해석이 가능한 딥러닝 결과물을 도출
  • 실용적으로 사용할 수 있는 해석 가능한 DL 구조를 만들고 싶음

 

모델 구조 (전체 구조)

N-Beats 모델은 인공 신경망 구조로, residual link와 FC(fully-connected) layer의 깊은 적층 구조(very deep stack)로 이루어져 있습니다.

 

전체 구조는 동일하나 해석이 가능한 구성요소를 포함시키는지 여부에 따라 두 가지로 나뉩니다.

• Generic Architecture
• Interpretable architecture

Input & Output

관측된 시점을 \(t\) 시점이라고 가정하면

• Output은 길이 \(H\)의 예측값 \([t+1,t+2,…t+H]\)
• Input은 길이가 \(nH\)인 관측값 \([t−nH,…,t−1,t]\)
  • \(n\) : hyper-parameter

본 논문에서는 \(n\)을 2~7로 설정하여 Input의 길이를 \(2H\)~\(7H\)로 활용

 

모델 구성요소

모델은 Basic Block과 Stack Block이 단계별로 구성되어 있습니다.

Stack은 여러 개의 Basic Block으로 이루어져 있으며, Double Residual Stacking으로 불리는 변형 Residual Connection으로 Stack 내에 있는 Block 끼리 연결되어 있습니다.

 

Basic Block 구조

Generic Basic Block 구조

Basic Block은 마지막 Backcast 함수, Forecast 함수가 어떤 것이냐에 따라 나뉩니다.

• Generic Basic Block
• Seasonal Basic Block
• Trend Basic Block

기본적인 구조는 동일하므로 Generic Basic Block을 통해 Basic Block이 어떻게 구성되어 있는지 설명해보겠습니다.

 

Input으로 15개의 관측 시점, Output으로 5개의 예측시점, Hidden size는 256, Theta size는 20이라고 가정하면

• Input으로 15개의 시점이 Stack1로 들어와 Stack1의 내부 Generic Basic Block \(l\)에 들어오면 우선 [FC+Relu]로 구성된 4개의 Layer를 통과하여 결과물로 256차원 벡터가 생성됩니다.
• 이 벡터는 각각 Backcast 경로와 Forecast 경로로 다시 분기되고, 분기된 백터는 한 번 더 FC layer를 거친 뒤 경로에 맞는 함수 \(g^b\) or \(g^f\)를 거쳐 Backcast 벡터(15차원==Input 크기)와 Forecast 벡터(5차원==Output 크기)가 생성됩니다.

Forecast 벡터의 의미는 해당 Block에서 생성한 예측값(5개)을 의미하고,

Backcast 벡터의 의미는 해당 Block에서 생성한 회귀 관측값(15개)을 의미합니다.

• FC는 Fully Connected Layer를 의미

 

Stack 구조

Stack은 여러 개의 Block으로 구성되어 있습니다.

 

각 Block으로부터 생성된 Backcast와 Forecast는 산술적 연산을 통해 Stack의 Output을 구성하거나 다음 Block Input으로 활용되는데, 이 구조가 Residual Connection과 닮아 있어 두 개이므로 Double Residual Stacking이라고 부릅니다.

 

자세한 산술식은 다음과 같습니다.

\(x_l = x_{l-1} - \hat {x_{l-1}}\)

• Stack 안에 있는 \(block_l\)의 input \(x_l\)은 이전 \(block_{l-1}\)의 input인 \(x_{l-1}\)에서 \(block_{l-1}\)을 통과하면서 생성된 Backcast 벡터 \(\hat{x_{l-1}}\)를 뺀 것과 같습니다.

\(\hat{y} = \sum_{l}\hat{y_l}\)

• Stack 안에 있는 \(l\)개의 Block으로부터 생성된 Forecast 벡터를 모두 더한 것이 Stack의 Output입니다.

 

이와 같은 구조는 아래와 같은 효과를 갖고 있습니다.

• Forcast와 Backcast에 적용된 Residaul Connection 구조는 Gradient의 흐름을 더 투명하게 하는 효과가 있습니다.
• Backcast의 Residual Connection 구조는 이전 Block이 Input의  일부 신호(signal)을 제거함으로써 다음 Block의 예측 작업을 쉽게 만드는 효과가 있습니다.
• Forcast의 Summation Connection 구조는 Input을 계층적으로 분해하는 효과를 갖고 있습니다.(Generic Basic Block에서는 큰 의미가 없을 수 있지만 뒤에 설명할 해석이 가능한 구조에서 큰 효과를 갖고 있음)

 

모델 구조

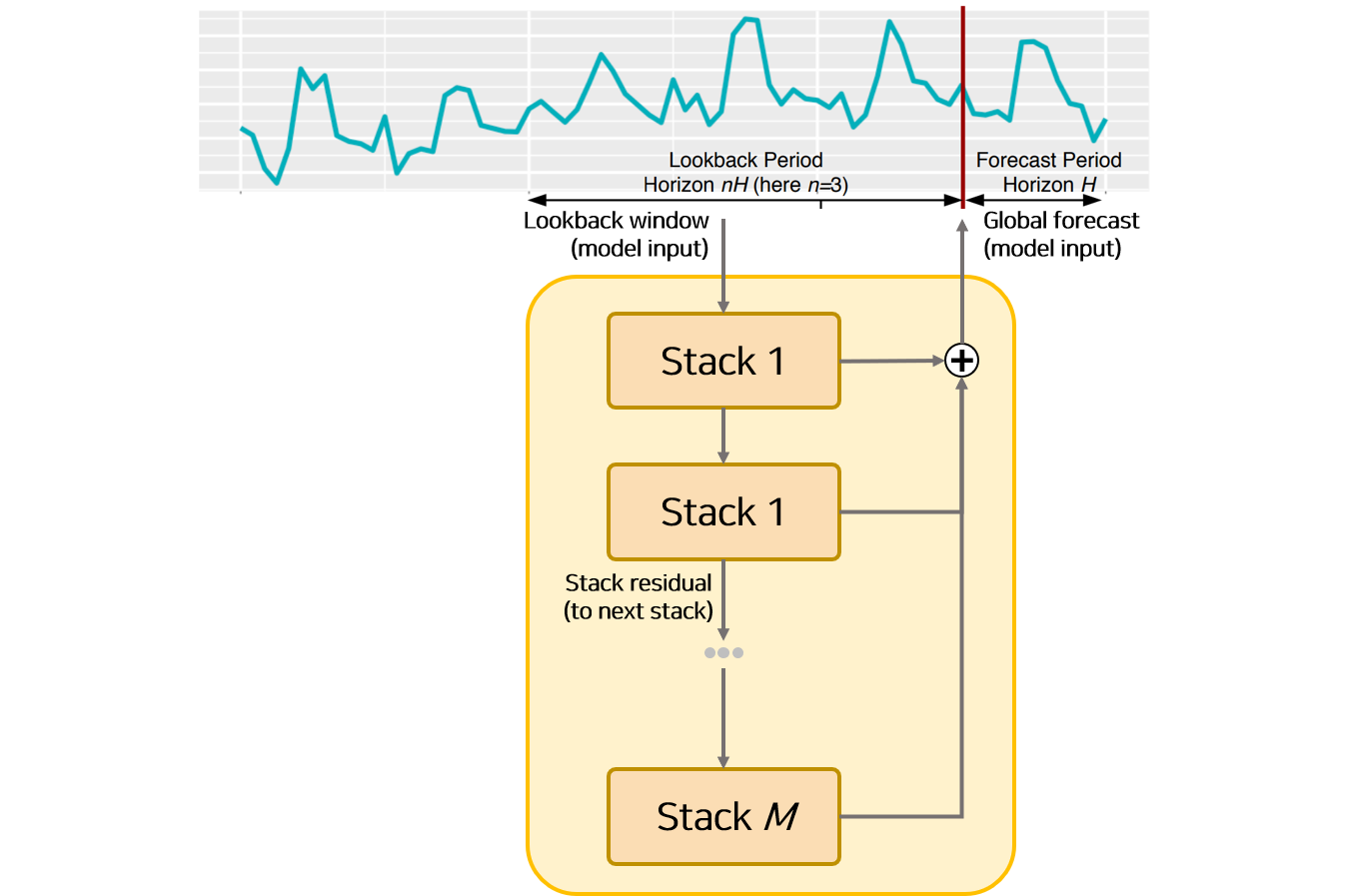
모델의 전체적 형태는 앞서 설명한 여러 개의 Stack으로 구성되어 있습니다.

 

Stack에서 설명한 것과 비슷하게 각 Stack에서 생성된 Backcast Output은 다음 Stack의 Input으로 활용됩니다.

그리고 모든 Stack에서 생성된 Forecast Output을 더한 값이 모델의 Output, 즉 길이 \(H\) 예측값입니다.

 

이 예측값과 실제값 차이를 나타내는 MSE(mean squared error)을 이용하여 Loss를 계산하고 Gradient Update하여 모델을 학습합니다.

 

해석이 가능한 모델 구조

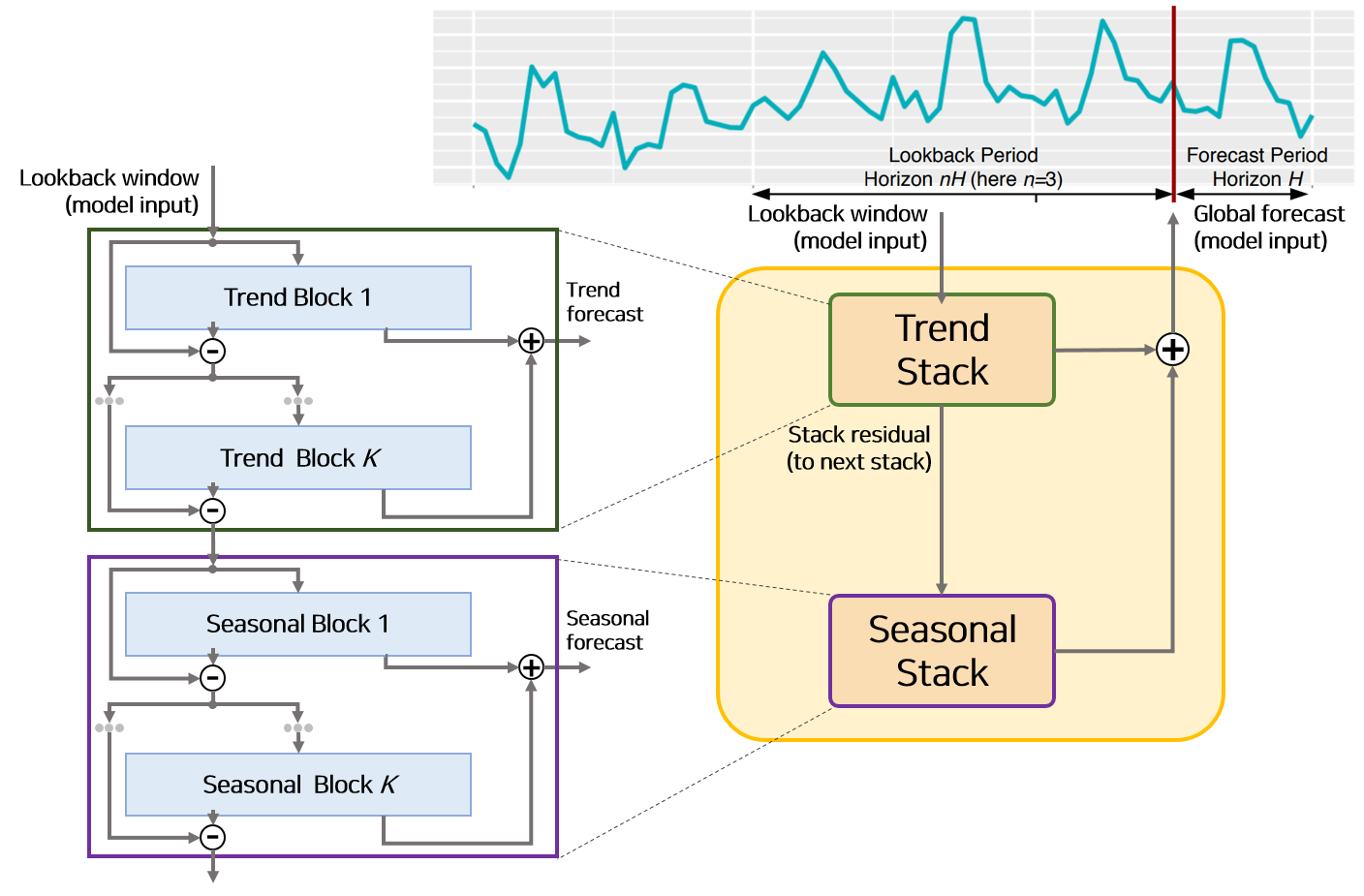
해석이 가능한 모델 구조는 전반적으로 앞서 설명한 모델의 구성요소를 모두 포함하고 있습니다.

 

다만 Basic Block의 구조에서 \(g^b\), \(g^f\) 함수가 학습 가능한 파라미터가 아니며 특수한 형태를 띄고 있습니다.

단조 증가함수 일 경우 Trend Block, 주기적 함수일 경우 Seasonal Block으로 나뉩니다.

 

해석이 가능한 모델은 이 Seasonal Block으로 이루어진 Seasonal Stack과 Trend Block으로 이루어진 Trend Stack 두 개가 그림의 순서대로 쌓여있는 구조로 구성되어 있습니다.

 

Trend Block & Trend Stack

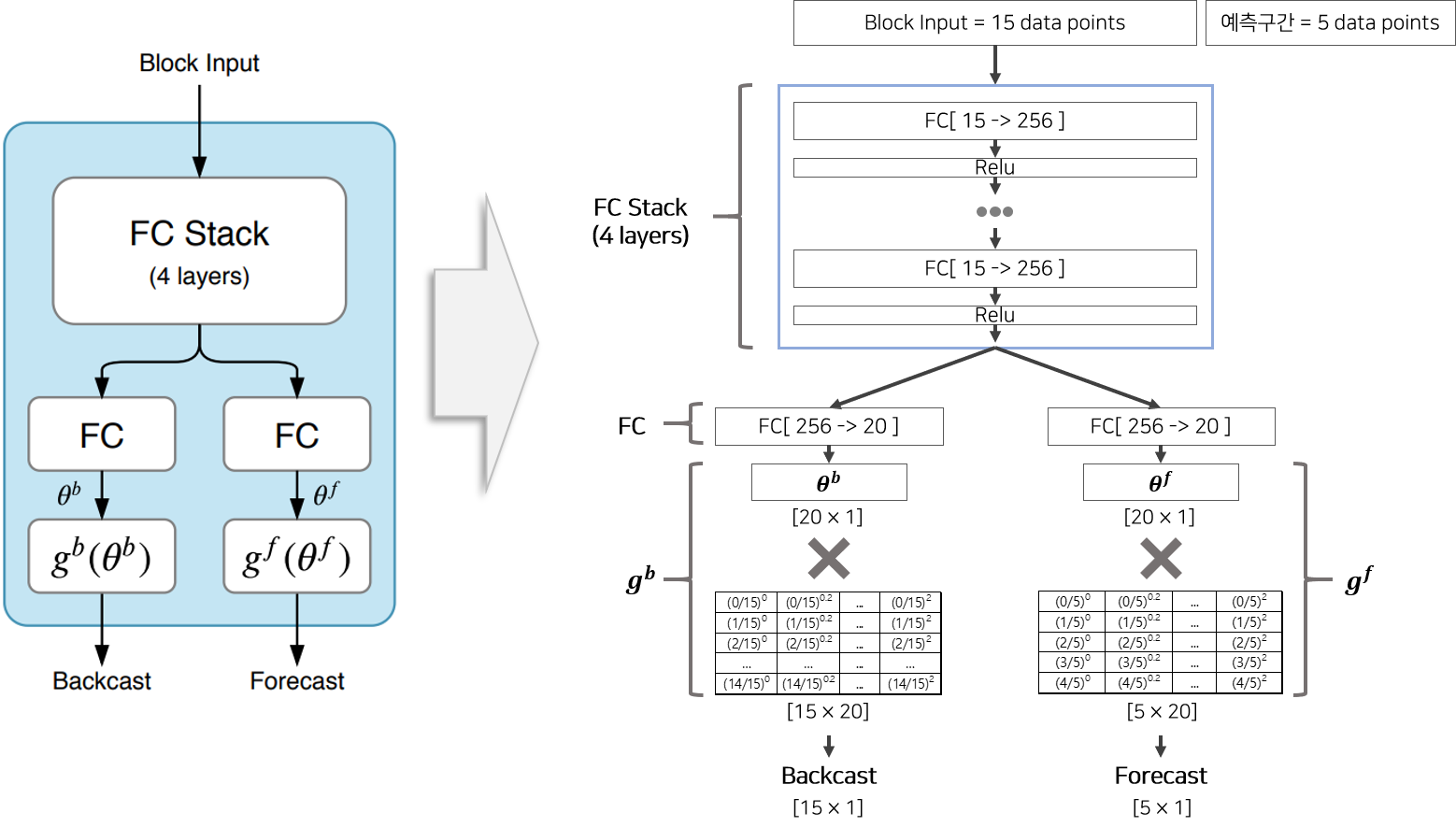
트렌드(Trend)의 사전적 의미는 어떤 방향으로 쏠리는 현상을 의미합니다.

즉 트렌드는 시간이 지남에 따라 서서히 단조증가 또는 단조감소와 같은 현상을 보여야 합니다.

 

따라서 이와 비슷한 Output을 생성할 수 있도록 Basic Block의 함수 \(g^b\), \(g^f\)을 변경한 것이 Trend Block입니다.

 

Block의 Forecast(\(\hat{y_l}\))를 구하는 수식은 아래와 같습니다.

• \(\hat{y_l}=T\theta^f_l\)
• \(T=[1, t, ..., t^p]\)
• \(t=[0, 1, ..., H-2, H-1]^T/H\)

생성된 Forecast(\(\hat{y_l}\)) 은 길이 H(그림에서는 5×1) 벡터인데 각 백터의 elements는 시간 순서의 예측값입니다.

즉 Trend Block으로부터 생성된 Forecast Output은 트렌드를 띄는 예측값을 생성합니다.

그리고 Trend Stack은 Trend Block으로 이루어진 Stack을 의미합니다.

 

Seasonal Block & Seasonal Stack

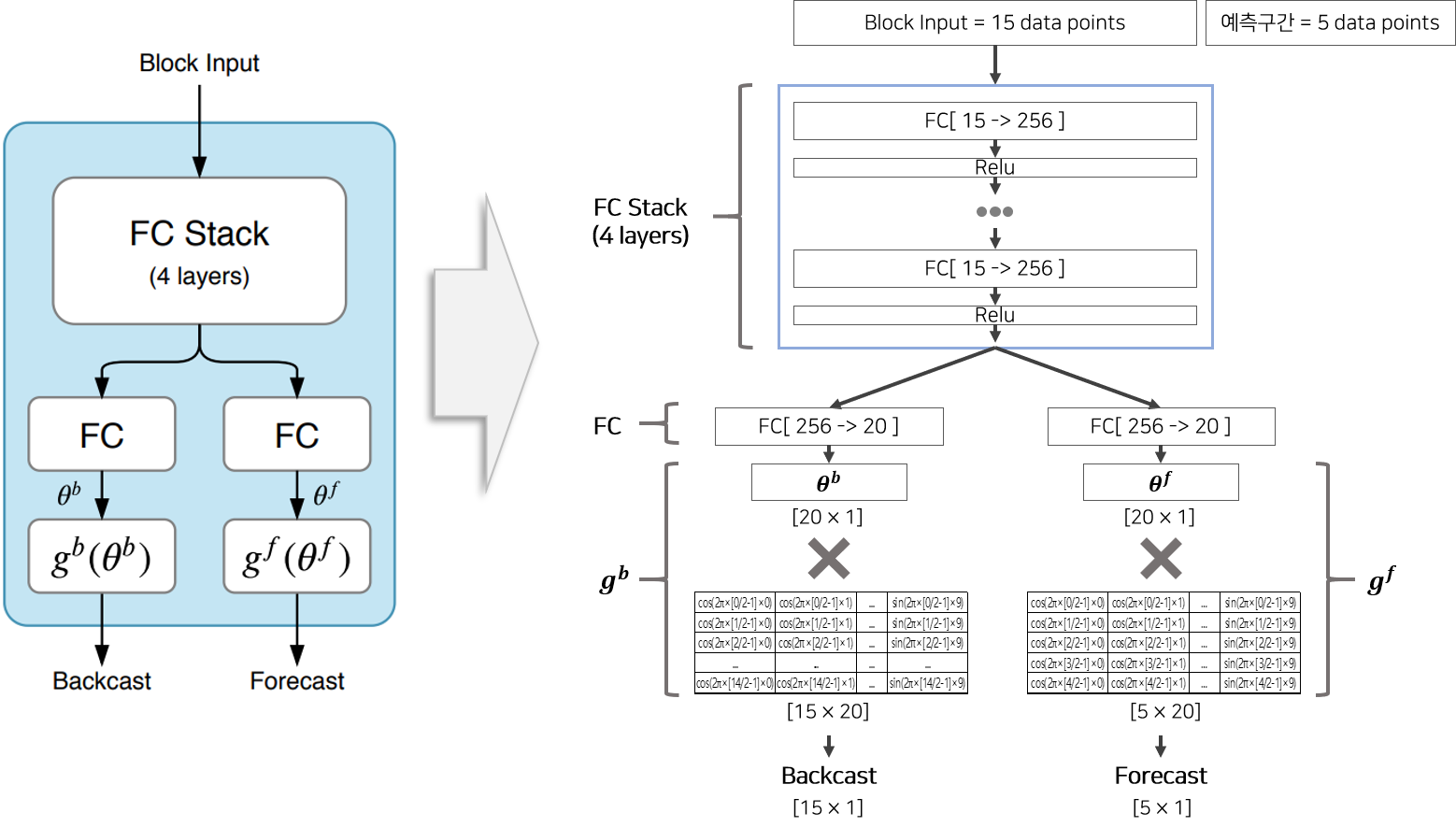
계절성(Seasonal)이란 주기성이 있으며 되풀이되는 특징을 갖고 있습니다.

따라서 계절성을 띄게 하도록 푸리에 급수(Fourier series) 를 모방하여 본 논문에서 주기 함수를 제시합니다.

 

즉 계절성을 띄도록 Basic Block의 함수 \(g^b\), \(g^f\)을 주기 함수로 변형한 것이 Seasonal Block입니다.

 

아래의 수식은 사인함수와 코사인함수 함수의 합으로 구성된 \(g^f\)의 모습입니다.

이 주기함수로 부터 생성된 Output은 시간에 따라 주기성을 띄는 벡터를 생성합니다.

• \(\hat{y_l}=S\theta^f_l\)
• \(S=[1, cos(2\pi t), ...,cos(2\pi[H/2-1]t), sin(2\pi t), ..., sin(2\pi[H/2-1]t)]\)

그리고 Seasonal Stack은 Seasonal Block으로 이루어진 Stack을 의미합니다.

 

실험 및 결과

본 논문은 M3, M4, TOURISM 단변량 데이터셋에서 테스트를 진행하였습니다.

앞에서 설명한 Block들을 이용하여 구성한 총 3가지 모델로 실험모델을 구성하고 다른 ML(Machine Learning), ST(Statical) 모델들과 비교합니다.

 

실험모델

• N-BEATS-G : Generic Basic Block만을 사용하여 구성한 N-Beats 모델
• N-BEATS-I : Sesonal Stack과 Trend Stack으로 구성된 해석 가능한 N-Beats 모델
• N-BEATS-I+G : N-BEATS-G과 N-BEATS-I의 앙상블 모델

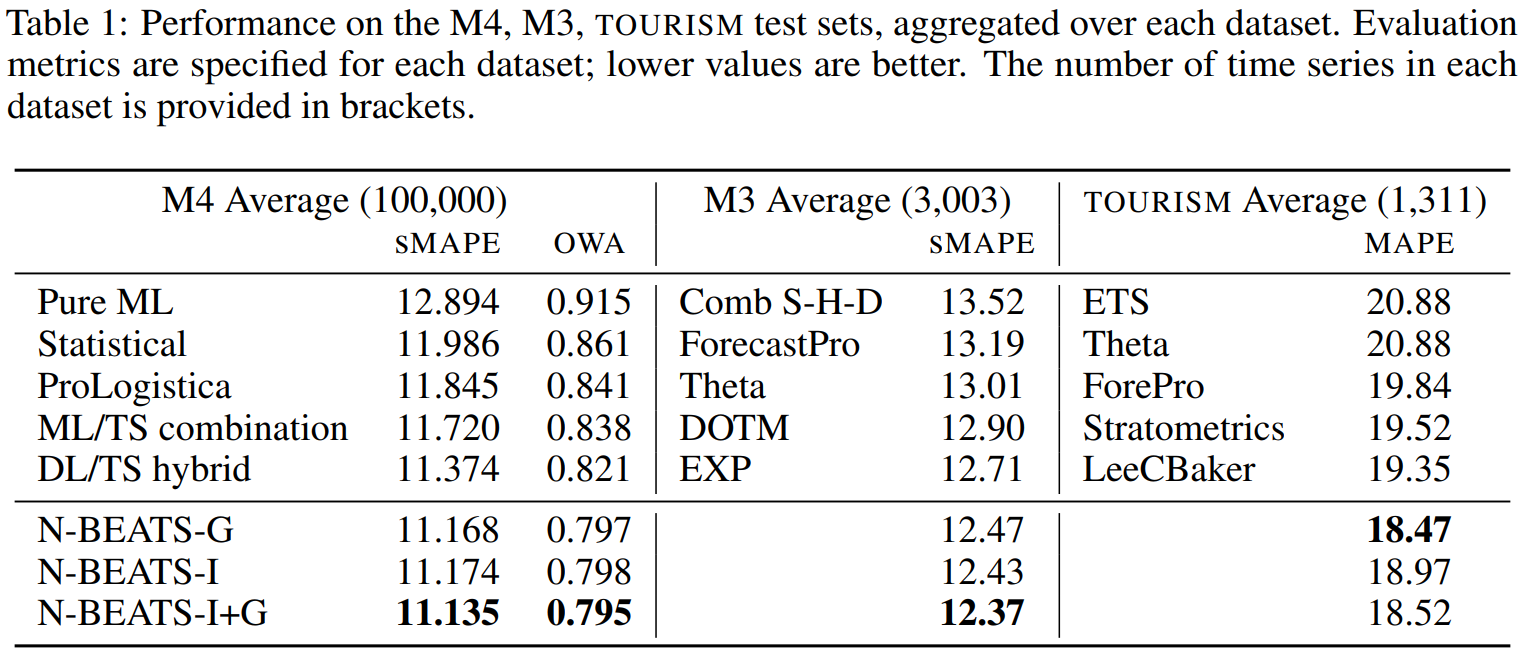
비교 모델 중 DL/TS hybrid는 M4 Competition에서 우승한 RS-RNN 모델입니다.

 

실험 결과를 통해 N-BEATS 모델이 다양한 평가 Metric으로 비교했을 때 비교 모델보다 모든 실험 데이터셋에서 가장 좋은 성능을 보인다는 것을 확인할 수 있습니다.

다른 비교 모델과는 다르게 스케일링이나 통계적 지식, 내부 구조 분석 등이 전혀 필요 없음에도 State of the Art(최첨단) 성능을 보였다는 것이 이 실험의 특징입니다.

 

Reference

해당 블로그 참고해서 작성했습니다.