[Paper Review] Self-Paced Learning for Latent Variable Models

Authors : Kumar, M., Packer, B., & Koller, D.

Journal/Conference : NeurIPS 2010

Source : https://proceedings.neurips.cc/paper/2010/file/e57c6b956a6521b28495f2886ca0977a-Paper.pdf

 

Background

잠재 변수 모델(Latent variable models)은 머신러닝의 몇몇 applications 좋은 성능을 보인다.

 

잠재 변수 모델의 매개변수를 학습하는 것은 종종 non-convex optimization problem를 해결할 필요가 있다.

이런 문제에서 근사적인 solution을 얻기 위한 몇 가지 접근법에는 잘 알려진 EM algorithm과 CCCP algorithm이 있다.

하지만 이런 접근 방식들은 high training과 일반화 오류로 인해 bad local minimum에 갇히기 쉽다.

 

non-covex optimization task를 해결하는 과정에서 bad local minimum에 빠지는 걸 피하기 위한 일반적인 접근 방식은 무작위 초기화와 함께 여러 번 실행해 보고 그중에서 가장 좋은 솔루션을 선택하는 것이다.

하지만 이런 방식은 확실하지 않을뿐더러 계산 비용이 많이 든다.

 

non-convex objective를 가진 훈련을 위한 대안적인 방법으로 Bengio가 제안한 Curriculum Learning이 있다.

이 아이디어는 쉬운 개념으로 시작하고 점차 복잡한 개념으로 학습하는 아이들이 학습하는 방식에서 영감을 받았다.

즉, 쉬운 샘플을 먼저 사용하고 점진적으로 더 복잡한 샘플을 학습한다.

(Curriculum Learning은 이전 글에 정리해 놓았다.)

 

Curriculum Learning을 사용하는 데 있어 주요 과제는 주어진 훈련 데이터 세트에서 쉽고 어려운 샘플을 식별해야 한다는 것이다.

하지만 샘플의 용이성에 대해 쉽게 계산할 수 있는 측정값이 제공되지 않는 경우가 많다.

 

이러한 훈련 샘플의 순위는 인간이 제공하기에 부담스럽거나 개념적으로 어려울 수 있고,

인간이 직관적으로 "쉽다" 생각하는 것은 기계가 "쉽다" 생각하는 것과 일치하지 않을 수 있다는 어려움이 존재한다.

 

Method

본 논문에서는 위에서 언급한 어려움을 완화하기 위해 self-paced learning 제안.

 

인간교육의 맥락에서 자율학습(self-paced learning)은 교사에 의해 고정되기보다는 학생의 능력에 의해 결정된다.

이러한 직관을 기반으로 각 iteration에서 동시에 쉬운 샘플을 선택하고 새로운 매개 변수 벡터를 학습하는 새로운 iterative self-paced learning 알고리즘을 제안.

• 각 iteration에서 선택된 샘플의 수는 나중의 iteration이 더 많은 샘플을 도입하도록 점진적으로 어닐링(annealing)되는 가중치에 의해 결정
• 모든 샘플을 고려하여 목적 함수를 더 이상 개선할 수 없을 때 수렴
• 여기서의 "쉬운" 것의 특성은 개별 샘플이 아니라 샘플 집합(표본 집합)에 적용됨

본 논문에서의 "쉽다"는 "옳은 결과를 예측하기 쉽다"로 정의한다.

즉, 목적함수 값이 작은 샘플이 쉬운 샘플이라 정의한다.

 

각 iteration에서 parameter \( w \)를 학습함과 동시에 쉬운 샘플을 선택하기 위해 기존 목적 함수를 수정한다.

기존 objective function

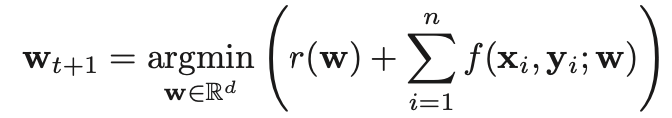
기존의 objective function에 \( i^{th} \) sample이 쉬운지 아닌지를 나타내는 \( v_i \)(binary variables)를 추가하여 목적함수를 수정한다.

제안 objective function

\( r(.) \) : regularization function

\( f(.) \) : negative log-likelihood 

 

학습 과정은 \( K \)를 결정한 후 \( v_i \)를 선택하고 w를 update 한다고 생각하면 된다.

 

위의 objective function을 정리하면 다음과 같다.

$$  \space r(w) + \sum^{n}_{i=1}v_{i}( \space f(x_i, y_i; w) - \frac{1}{K}) $$

• \( f(x_i, y_i; w) \leq \frac{1}{K} \) : 목적 식을 감소시키는데 기여하므로 학습에 포함 -> \( v_i \) = 1
• \( f(x_i, y_i; w) \geq \frac{1}{K} \) : 목적 식을 감소시키는데 기여하지 못하므로 학습에 포함되지 않음 -> \( v_i \) = 0

 

\( K \) : 학습에 고려될 샘플의 수를 결정하는 weight

• \( f(x_i, y_i; w) \leq \frac{1}{K} \)인 샘플들만 학습에 포함되므로 \( frac{1}{K} \)가 작으면 적은 수의 샘플만 학습에 포함됨
• \( K \)를 점차 줄여 0에 가까워지며 더 많은 샘플들을 학습에 포함.

처음에는 적은 데이터(쉬운 데이터)로 시작해서 모든 데이터들이 학습에 사용될 때까지 점진적으로 사용되는 샘플의 수를 늘려간다.

 

Conclusion

본 연구의 골자

• 반복적으로 쉬운 샘플을 선택하고 동시에 parameter를 업데이트하는 방식으로 biconvex optimization problem을 해결.
• 기존 curriculum learning에서 한계점이었던 쉬운 샘플들을 선정하는 방식을 제안.
• 4가지 applications(Noun Phrase Coreference, Motif Finding, Handwritten Digit Recognition, Object Localization)에서 latent SSVM을 학습하는 CCCP algorithm보다 성능이 좋음을 보임.

 

Reference

Kumar, M., Packer, B., & Koller, D. (2010). Self-paced learning for latent variable models. Advances in neural information processing systems, 23.

 

http://dmqm.korea.ac.kr/activity/seminar/338