회귀 (Regression)
회귀는 보통 연속적인 숫자, 예측값이 float 형태인 문제들을 해결하는 데 사용됩니다.
즉, 회귀는 출력 값에 연속성이 있습니다.
train data를 가장 잘 나타낼 수 있는 선형(Linear) 모델을 생성 후 예측을 진행합니다.
아래에서 자세히 설명하겠습니다.
예시 : 공부에 투자한 시간(x)을 바탕으로 시험 점수(y)(0~100) 예측
모델(가설)
H(x) = Wx + b
- H(x) : 우리가 가정한 가설(Hypothesis)
- W : 가중치 (Weight)
- b : 편향값 (bias)
x(특성(Feature), 설명변수)가 하나인 경우를 단순 선형 회귀(Simple Linear Regression)이라 하고,
x가 2개이상인 경우를 다중 선형 회귀(Multiple Linear Regression)이라 합니다.


비용 함수(Cost function / Loss function)
train data에 잘 맞는 직선을 어떻게 만들지 생각해봅시다.
train data의 true값(y)과 직선에 x를 넣어서 나온 값 H(x) 값의 거리를 구하여 작으면 잘 만든 직선이라고 생각합니다.
- y(true)와 H(x)의 거리로 판단.
- Distance(거리) : (H(x) - y)^2
- 거리는 차이를 모두 양수로 표현하고, 차이가 클 때 penalty를 많이 주기 위해 보통 제곱을 사용합니다.

train data에 잘 맞는 직선을 만들기 위해서는 하나의 x값에 대해서만 판단하는 것이 아니라 모든 instance를 고려해야 할 것입니다.
비용 함수는 모든 instance의 거리의 평균으로써, 평균 제곱 오차(Mean Squared Error, MSE)입니다.

※ instance의 수 = data의 수
※ m은 instance의 개수라고 생각하시면 됩니다.
아까 위에서 H(x)를 W와 b에 대한 식으로 구현했기 때문에 비용 함수는 W, b에 대한 함수가 될 것입니다.
결론적으로, 비용함수는 작을수록 좋다고 판단하고, 비용 함수는 W와 b에 대한 함수이기 때문에
저희의 최종목표는 비용 함수를 최소화하는 W와 b를 찾는 것입니다.

경사 하강법(Gradient descent algorithm)
그러면 어떻게 비용함수를 최소화하는 W와 b를 찾을지 생각을 해봐야 합니다.
비용 함수를 보면 제곱을 했기 때문에 W에 대한 이차함수, b에 대한 이참 함수입니다.
W에 대한 식으로 보자면 다음과 같은 그래프일 것입니다.

다시 한번 상기해보면 비용 함수(Cost)를 최소화하는 W를 찾아야 하는 것이 저희의 목표입니다.
위의 그래프에서는 W=1일 때 Cost가 최소가 되는 걸 볼 수 있습니다.
경사 하강법은 비용함수의 최솟 값을 가지도록하는 W를 찾는 알고리즘입니다. 과정은 다음과 같습니다.
- 임의의 초기값 W을 정합니다.
- W를 조금씩 수정하면서 Cost를 줄이는 방향으로 진행합니다.
- Cost를 가능한 많이 줄이는 방향으로 진행합니다.
- 계속 반복하며 Cost의 최솟 값을 찾습니다.

주목할 것은 아래로 갈수록 접선의 기울기가 점차 작아진다는 점입니다.
그리고 마지막의 최솟값에서는 접선의 기울기가 0이 되게 됩니다.
경사하강법은 비용 함수를 W에 대해 미분하여 현재 W에서의 접선의 기울기를 구하고,
접선의 기울기의 반대 방향으로 진행하여 W값을 수정하는 것은 반복하며 Cost를 최소화하는 W를 찾습니다.

- α : 얼마나 움직일지 조절하는 상수 -> 적당한 α 선택도 중요.
- α 뒤의 식은 비용함수 W에 대해 미분한 식 즉, 접선의 기울기
※ 주목할 점은 ' - ' 가 있어 기울기의 반대 방향으로 움직인다는 점
다중 선형 회귀에서의 matrix 표현
다중 선형 회귀는 Feature가 여러 개인 경우이므로 H(x) 값에 계수도 여러 개가 필요합니다.
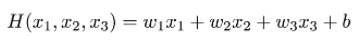
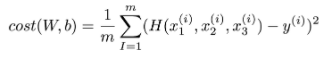
위의 경우는 Feature가 3개라 저런 식으로 표현해도 괜찮아 보이지만, 특성의 수가 많아지면 점점 표현하기 힘들 것입니다.
Matrix의 행렬곱을 사용하면 쉽게 표현할 수 있다.
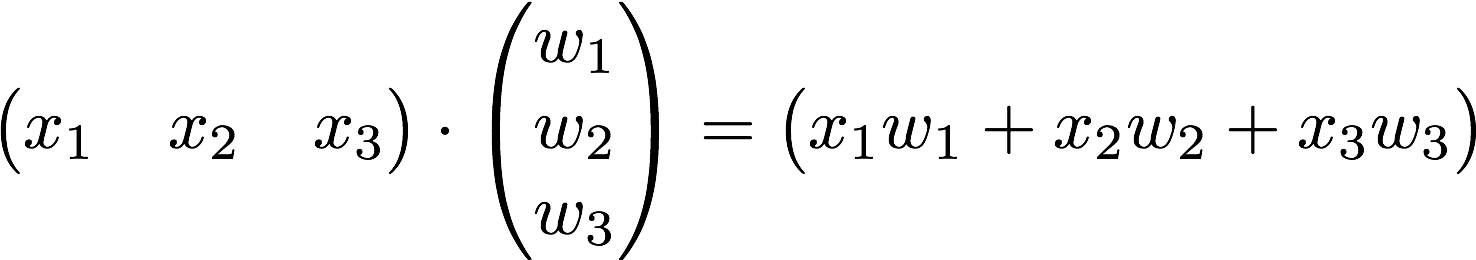
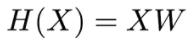
더 구체적으로 instance의 개수까지 고려하게 되면 다음과 같다.
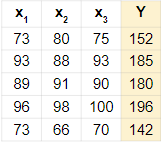
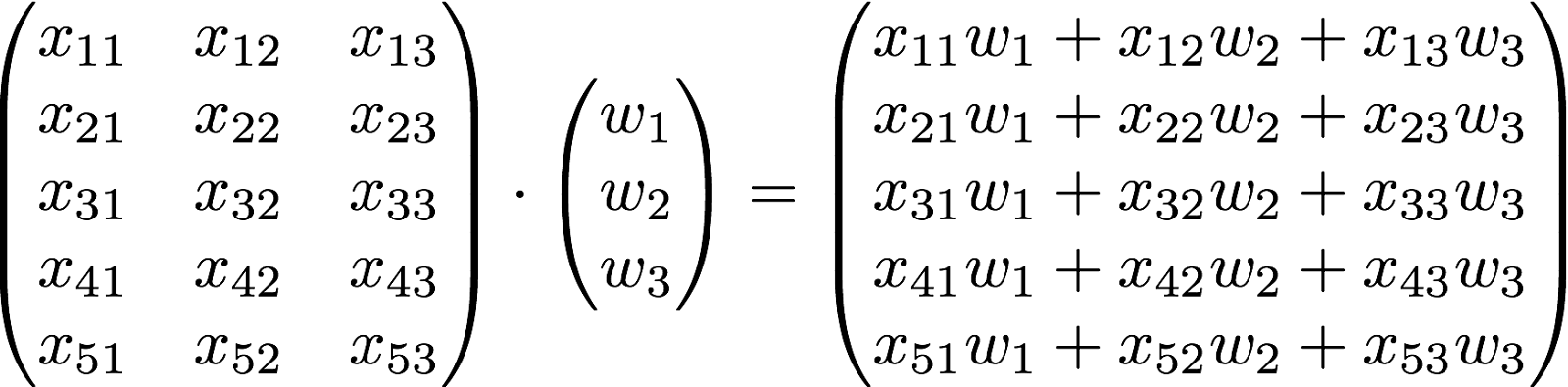
instance와 Feature의 수, label의 수를 고려해서 W의 shape을 결정하면 됩니다.
다음은 label이 두 개 있을 경우 예시입니다.
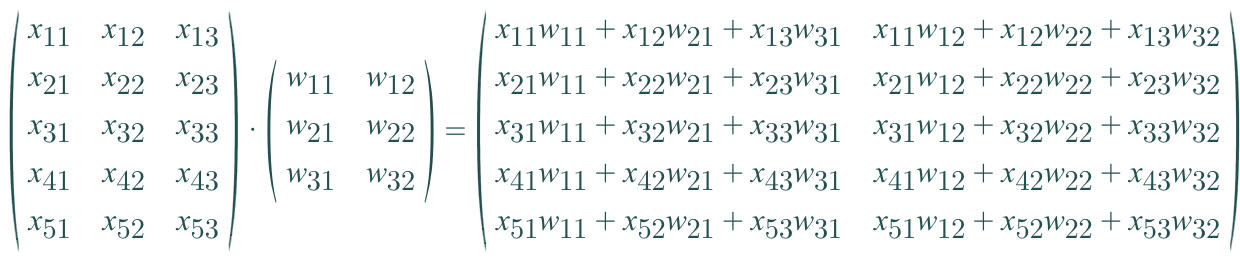
Reference
본 글은 김성훈 교수님의 강의와 강의자료를 토대로 작성했습니다.
https://www.youtube.com/playlist?list=PLlMkM4tgfjnLSOjrEJN31gZATbcj_MpUm
모두를 위한 딥러닝 강좌 시즌 1
www.youtube.com
'Data Science > Machine Learning' 카테고리의 다른 글
| [ML] Clustering (군집화) - K-Means, Hierarchical Clustering (0) | 2022.06.29 |
|---|---|
| [ML] 분류(Classification) (2) | 2022.02.06 |
| [ML] 머신러닝(Machine Learning)이란? (0) | 2022.02.06 |
| [ML] 결정 트리 (Decision Tree) (0) | 2022.02.01 |




댓글