Clustering
- Target 변수(y 변수)가 없는 데이터 분석법
- unsupervised machine learning task
- clustering algorithms only interpret the input data and find natural groups or clusters in feature space
- 전체적인 데이터의 구조를 파악하는데 이용
- Unsupervised이므로 clustering 결과에 대해 정확도를 알 수 있는 방법은 없음 (정답이 없으므로)
- Clustering만의 평가방법이 따로 존재
- 군집분석은 자료 사이의 거리를 이용하여 수행되기 때문에, 각 자료의 단위가 결과에 큰 영향을 미침
- 그렇기 때문에 표준화를 진행
군집의 평가방법
실루엣 분석( Silhouette analysis)
비지도 학습의 특성상 어떠한 지표라도 정확하게 성능을 평가하기는 어려움이 있습니다.
그럼에도 불구하고 군집화의 성능을 평가하는 대표적인 방법으로는 실루엣 분석을 자주 활용합니다.
실루엣 분석은 각 군집 간의 거리가 얼마나 효율적으로 분리돼 있는지를 나타냅니다.
효율적으로 잘 분리됐다는 것은 다른 군집과의 거리는 떨어져 있고 동일 군집끼리의 데이터는 서로 가깝게 잘 뭉쳐있다는 의미입니다.
실루엣 분석은 실루엣 계수를 기반으로 합니다.
- 실루엣 계수 : 개별 데이터가 가지는 군집화 지표
- 개별 데이터가 가지는 실루엣 계수는 해당 데이터가 같은 군집 내의 데이터와 얼마나 가깝게 군집화돼 있고, 다른 군집에 있는 데이터와는 얼마나 멀리 분리돼 있는지를 나타내는 지표
- 전체 데이터의 실루엣 계수 값의 평균이 높을수록 군집화가 어느 정도 잘 됐다고 판단할 수 있지만 무조건 이 값이 높다고 해서 군집화가 잘 됐다고 판단할 수는 없음
특정 데이터 포인트의 실루엣 계수 값
\(s(i) = \frac{b(i) - a(i)}{max(a(i),b(i))}\)
- a(i) : 해당 데이터 포인트와 같은 군집 내에 있는 다른 데이터 포인트와의 거리를 평균한 값
- 작을수록 좋음
- b(i) : 해당 데이터 포인트가 속하지 않은 군집 중 가장 가까운 군집과의 평균 거리
- 클수록 좋음
- b(i) - a(i) : 두 군집 간의 거리가 얼마나 떨어져 있는가의 값
- max(a(i), b(i)) : 정규화하기 위해 나누어줌
좋은 군집화의 조건은 다음과 같습니다.
- 전체 실루엣 계수의 평균값은 0 ~ 1 사이의 값을 가지며, 1에 가까울수록 좋음
- 하지만 전체 실루엣 계수의 평균값과 더불어 개별 군집의 평균값의 편차가 크지 않아야 함. 만약 전체 실루엣 계수의 평균값은 높지만, 특정 군집의 실루엣 계수 평균값만 유난히 높고 다른 군집들의 실루엣 계수 평균값은 낮으면 좋은 군집화 조건이 아님
- 즉, 개별 군집의 실루엣 계수 평균값이 전체 실루엣 계수의 평균값에서 크게 벗어나지 않는 것이 중요함
Model
- Hierarchical clustering
- K-Means
- 거리 기반 군집화
- GMM
- 확률 기반 군집화
K-Means
K-Means Clustering는 사전에 결정된 군집수 k에 기초하여 전체 데이터를 상대적으로 유사한 k개의 군집으로 구분합니다.
- 군집수 k를 결정
- 초기 Centroid를 정함
- Centroid로부터 가장 가까이에 있는 자료들을 같은 cluster로 묶음
- Centroid의 위치를 cluster의 가운데 지점(중심)으로 옮김
- Data가 총 두 개뿐이라면, Centroid는 다른 데이터 위로 겹쳐서 올린다
- 더 이상 assign이 되지 않을 때까지 반복 (Iteration)
Determination of K
- K-Means clustering의 결과는 초기 군집수 k의 결정에 민감하게 반응한다.
- 여러 가지의 k값을 선택하여 군집 분석을 수행한 후 가장 좋다고 생각되는 k값을 이용
- Elbow point 계산하여 K 선택
- Silhouette plot으로 K 선택
- 자료의 시각화를 통하여 K 선택
- 자료의 시각화를 위하여 차원의 축소가 필수적이고, 이를 위하여 주성분 분석방법이 널리 이용됨
- 대용량 데이터에서 Sampling 한 데이터로 계층적 군집 분석을 우선 수행하여, K값을 선택
중심 초기값 설정 (Centorid decision)
- K-mean++
- 가장 맨 처음 data를 centorid로 지정
- 1st centorid에서 제일 먼 data를 2번째 centorid로 지정
- 1st와 2nd centroids에서 가장 먼 data를 3rd로 설정
- Random 하게 선택
- 문자 그대로 random 하게 centroid를 흩뿌림
- 사용자가 임의로 지정
장점
- 일반적인 군집화에서 가장 많이 활용되는 알고리즘
- 알고리즘이 쉽고 간결
단점
- 거리 기반 알고리즘으로 속성의 개수가 매우 많을 경우 군집화 정확도가 떨어짐
- 이를 위해 PCA로 차원 감소를 적용해야 할 수도 있음
- 반복 횟수가 많을 경우 수행 시간이 매우 느려짐
- 몇 개의 군집(cluster)을 선택해야 할지 가이드하기가 어려움
Hierachical clustering (계층적 군집분석)
비슷한 군집끼리 묶어 가면서 최종적으로는 하나의 케이스가 될 때까지 군집을 묶는 클러스터링 알고리즘입니다.
K-Means와는 다르게 군집의 수를 미리 정해주지 않아도 된다는 장점이 존재합니다.
- 주어진 데이터에서 모든 두 군집 간의 거리를 계산하는 알고리즘 (데이터의 이진트리 구성)
- 가장 가까운 거리에 있는 데이터를 서로 묶음 (반복 수행)
- 최종적으로 하나의 클러스터로 합쳐질 때까지 진행
- Dendrogram 형태의 자연적인 계층 구조로 정렬
Cluster Linkage
두 클러스터 간 거리 측정에서 기준점 삼을 데이터를 결정하는 방법입니다.
Linkage 알고리즘에 따라 클러스터 형태가 다르기에, 주어진 데이터에 적절한 Cluster Linkage를 적용해야 합니다.
- Single Linkage
- 각 클러스터 내 데이터 사이의 가장 긴 거리를 두 클러스터 사이의 거리로 생각
- 즉, 가장 비슷하지 않은 두 데이터의 거리를 두 클러스터 사이의 거리로 정의
- Complete Linkage
- 각 클러스터 내 데이터 사이의 가장 긴 거리를 두 클러스터 사이의 거리로 생각
- 즉, 가장 비슷하지 않은 두 데이터의 거리를 두 클러스터 사이의 거리로 정의
- Average Linkage
- 클러스터 내 모든 데이터와 다른 클러스터 내 모든 데이터 사이의 거리 평균을 두 클러스터 사이의 거리로 생각
- Centroid Linkage
- 각 클러스터의 중앙값 사이의 거리를 두 클러스터 사이의 거리로 생각
Dendrogram
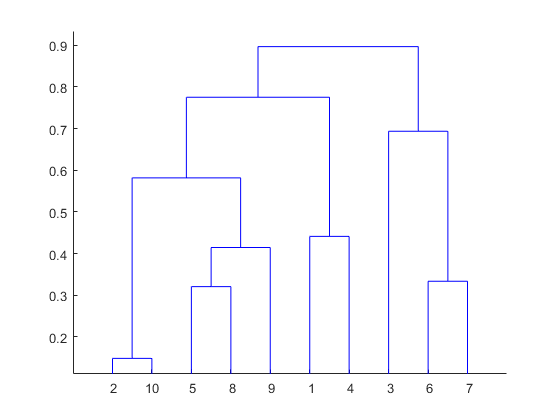
덴드로그램은 클리스터링의 결과를 시각화하기 위한 대표적인 그래프입니다.
대표적으로 계층적 군집분석(hierachical clustering) 방식에 대해 시각화하는 그래프로 많이 활용되고 있습니다.
장점
- 군집의 수를 알 필요가 없음
- 덴드로그램을 통해 군집화 프로세스와 결과물을 표현 가능
단점
- 계산속도가 느림
- 이상치가 존재할 경우, 초기 단계에 잘못 분류된 군집은 분석이 끝날 때까지 소속군집이 변하지 않음
- 이상치에 대한 사전검토 필요, Centroid 방법이 이상치에 덜 민감
'Data Science > Machine Learning' 카테고리의 다른 글
| [ML] 회귀 (Regression)와 경사하강법 (Gradient descent) (0) | 2022.02.22 |
|---|---|
| [ML] 분류(Classification) (2) | 2022.02.06 |
| [ML] 머신러닝(Machine Learning)이란? (0) | 2022.02.06 |
| [ML] 결정 트리 (Decision Tree) (0) | 2022.02.01 |




댓글