반응형
활성화 함수 (Activation Function)
활성화 함수란 입력 신호의 총합을 출력 신호로 변환하는 함수입니다.
본 글에서는 활성화 함수의 종류 중 시그모이드(sigmoid) 함수와 ReLU 함수, 계단(step) 함수에 대해서 알아보겠습니다.

계단 함수(Step Function)
계단 함수는 임계값을 경계로 출력이 바뀌는 활성화 함수입니다.
퍼셉트론에서는 활성화 함수로 계단 함수를 이용합니다.
import numpy as np
import matplotlib.pylab as plt
def step_function(x):
return np.array(x > 0, dtype=np.int)
X = np.arange(-5.0, 5.0, 0.1)
Y = step_function(X)
plt.plot(X, Y)
plt.ylim(-0.1, 1.1) # y축의 범위 지정
plt.show()
시그모이드 함수(Sigmoid Function)
신경망에서는 활성화 함수로 시그모이드 함수를 이용하여 신호를 변환하고, 그 변환된 신호를 다음 뉴런에 전달합니다.
퍼셉트론과 신경망의 주된 차이는 이 활성화 함수뿐입니다.
그 외에 뉴런이 여러 층으로 이어지는 구조와 신호를 전달하는 방법은 기본적으로 퍼셉트론과 동일합니다.

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
def sigmoid(x):
return 1 / (1 + np.exp(-x))
x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()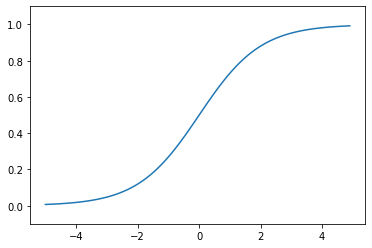
계단 함수와 시그모이드 함수 비교
차이점
- 매끄러움의 차이
- 시그모이드 함수는 부드러운 곡선 → 출력이 연속적으로 변화
- 계단 함수는 임계값을 경계로 출력이 바뀌어 버림
- 계단 함수는 0과 1을 리턴 하지만, 시그모이드 함수는 실수를 리턴
공통점
- 큰 관점에서 보면 둘은 같은 모양을 하고 있음
- 둘 다 입력이 작을 때의 출력은 0에 가깝고, 입력이 커지면 출력이 1에 가까워짐
- 입력이 아무리 작거나 커도 출력은 0에서 1 사이
- 모두 비선형 함수
# coding: utf-8
import numpy as np
import matplotlib.pylab as plt
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def step_function(x):
return np.array(x > 0, dtype=np.int)
x = np.arange(-5.0, 5.0, 0.1)
y1 = sigmoid(x)
y2 = step_function(x)
plt.plot(x, y1)
plt.plot(x, y2, 'k--')
plt.ylim(-0.1, 1.1) # y축 범위 지정
plt.show()
ReLU 함수(ReLU Function)
시그모이드 함수는 신경망 분야에서 오래전부터 이용해왔으나
최근에는 ReLU(Rectified Linear Unit) 함수를 주로 이용합니다.
ReLU는 입력이 0을 넘으면 그 입력을 그대로 출력하고, 0 이하면 0을 출력하는 함수입니다.
import numpy as np
import matplotlib.pylab as plt
def relu(x):
return np.maximum(0, x)
x = np.arange(-5.0, 5.0, 0.1)
y = relu(x)
plt.plot(x, y)
plt.ylim(-1.0, 5.5)
plt.show()
Reference
본 글은 밑바닥부터 시작하는 딥러닝을 참고하여 작성하였습니다.
반응형
'Data Science > Deep Learning' 카테고리의 다른 글
| [DL] 오차역전파법(Backpropagation) (2) | 2022.03.08 |
|---|---|
| [DL] 신경망 학습 (0) | 2022.03.04 |
| [DL] 손실함수 (Loss Function) : 오차제곱합(SSE), 교차 엔트로피 오차(Cross-Entropy) (0) | 2022.03.04 |
| [DL] 신경망(Neural network) (0) | 2022.02.25 |
| [DL] 퍼셉트론(Perceptron) (0) | 2022.02.24 |




댓글