퍼셉트론에서 신경망으로
편향을 명시한 퍼셉트론의 형태는 다음과 같습니다.
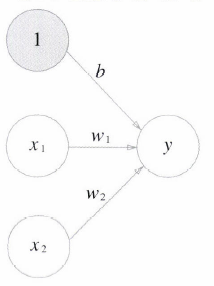
관련 식을 간결한 형태로 작성하면 다음과 같습니다.

- 입력 신호의 총합이 h(x)라는 함수를 거쳐 변환되어, 그 변환된 값이 y의 출력이 됩니다.
- h(x) : 입력이 0을 넘으면 1을 돌려주고, 그렇지 않으면 0을 돌려주는 함수입니다.
활성화 함수 (Activation function)


h() : 입력 신호의 총합을 출력 신호로 변환하는 함수입니다.
2단계로 처리합니다.
- 가중치가 곱해진 입력 신호의 총합을 계산
- 그 합을 활성화 함수에 입력해 결과(y)를 냄
자세하게 살펴보면 가중치 신호를 조합한 결과가 a라는 노드가 되고, 활성화 함수 h()를 통과하여 y라는 노드로 변환되는 과정입니다.
신경망의 동작을 더 명확히 드러내고자 할 때는 활성화 처리 과정을 명시하기도 합니다.
※ 이 책에서는 뉴런과 노드라는 용어를 같은 의미로 사용했습니다.
신경망의 예시
입력이 2개, 출력이 2개인 '2층 신경망'의 기본적인 형태은 다음과 같습니다.

- 가장 왼쪽 줄 : 입력층
- 맨 오른쪽 줄 : 출력층
- 중간 줄 : 은닉층
- 은닉충의 뉴런은 입력층이나 출력층과 달리 사람 눈에는 보이지 않습니다.
- 순서대로 0층, 1층, 2층
- 3층으로 구성 → 가중치를 갖는 층은 2개뿐이기 때문에 ‘2층 신경망’이라 합니다.
신경망의 활성화 함수
신경망에서는 활성화 함수로 비선형 함수를 사용해야 합니다.
선형 함수를 이용하면 신경망의 층을 깊게 하는 의미가 없어지기 때문입니다.
선형 함수의 문제는 층을 아무리 깊게 해도 ‘은닉층이 없는 네트워크’로도 똑같은 기능을 함수 있다는 데 있습니다.
층을 쌓는 혜택을 얻고 싶다면 활성화 함수로는 반드시 비선형 함수 사용해야 합니다.
신경망에서는 활성화 함수로 시그모이드 함수를 이용하여 신호를 변환하고, 그 변환된 신호를 다음 뉴런에 전달합니다.
퍼셉트론과 신경망의 주된 차이는 이 활성화 함수뿐입니다.
그 외에 뉴런이 여러 층으로 이어지는 구조와 신호를 전달하는 방법은 기본적으로 퍼셉트론과 동일합니다.
활성화 함수의 종류에 대해서는 다음 글에 작성했습니다. 참고 부탁드립니다.
https://wannabenice.tistory.com/16
[DL] 활성화 함수 - 시그모이드(sigmoid), ReLU, 계단함수
활성화 함수 (Activation Function) 활성화 함수란 입력 신호의 총합을 출력 신호로 변환하는 함수입니다. 본 글에서는 활성화 함수의 종류 중 시그모이드(sigmoid) 함수와 ReLU 함수, 계단(step) 함수에 대
wannabenice.tistory.com
3층 신경망 구현
입력층(0층), 은닉층(1층), 은닉층(2층), 출력층(3층)으로 구성
예를 들어,
- 입력층 : 2개의 뉴런
- 첫 번째 은닉층(1층) : 3개의 뉴런
- 두 번째 은닉층(2층) : 2개의 뉴런
- 출력층(3층) : 2개의 뉴런
으로 구성된 3층 신경망을 살펴보겠습니다.
편향을 뜻하는 뉴런을 추가하면 다음과 같이 구성될 것입니다.


행렬의 곱을 사용하면 다음과 같이 표현 가능합니다.


- 대응하는 차원의 수가 맞아야 합니다.
입력층에서 1층으로의 신호 전달에서 활성화 함수에서의 처리를 살펴보겠습니다.


- 은닉층에서의 가중치 합 (가중 신호와 편향의 총합)을 a로 표시
- 활성화 함수 h( )로 변환된 신호를 z로 표기
- 활성화 함수로 시그모이드 함수 사용
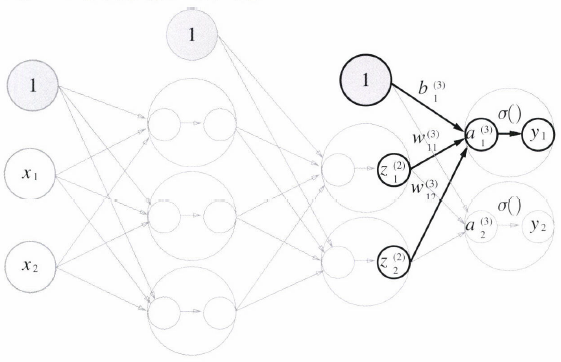
- 입력층->1층, 1층->2층의 구현과 거의 같습니다.
- 활성화 함수만 지금까지의 은닉층과 다릅니다.
- 출력층의 활성화 함수는 σ()로 표시하여 은닉층의 활성화 함수 h()와는 다름을 명시합니다. (σ : 시그마)
- 출력층의 활성화 함수는 풀고자 하는 문제의 성질에 맞게 정합니다.
- 예를 들어,
- 회귀에는 항등 함수 (입력을 그대로 출력하는 함수)
- 2 클래스 분류에는 시그모이드 함수
- 다중 클래스 분류에는 소프트맥스 함수를 사용하는 것이 일반적
위의 3층 신경망 구현은 신호가 순방향으로 전달됩니다.
(순 전파, 입력에서 출력 방향으로)
출력층 설계
신경망은 분류와 회귀 모두에 이용할 수 있습니다.
다만 둘 중 어떤 문제냐에 따라 출력층에서 사용하는 활성화 함수가 달라집니다.
일반적으로 회귀에는 항등 함수를, 분류에는 소프트맥스 함수를 사용합니다.
항등 함수(identity function)
- 입력을 그대로 출력
- 입력과 출력이 항상 같다는 뜻의 항등

소프트맥스 함수(softmax function)
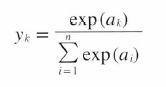
- n : 출력층의 뉴런 수
- yk : k번째 출력
- ak : 입력 신호
- 분자 : 입력 신호 ak의 지수 함수
- 분모 : 모든 입력 신호의 지수 함수의 합

출력층의 각 뉴런이 모든 입력 신호에서 영향을 받기 때문에 이와 같이 표현됩니다.
def softmax(a):
exp_a = np.exp(a)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
소프트맥스 함수 구현 시 주의점
위의 코드는 식을 제대로 표현하고 있지만, 컴퓨터로 계산할 때는 결함이 있습니다.
오버플로 문제인데, 지수 함수를 사용하기 때문에 엄청나게 큰 값이 나올 때, 범위를 넘어가면 inf를 반환하기도 해서 문제가 생깁니다.
다음과 같이 소프트맥스 함수 구현을 개선하면 문제가 해결됩니다.

C’ 값은 오버플로를 막을 목적으로 입력 신호 중 최댓값을 이용하는 것이 일반적입니다.
def softmax(a):
c = np.max(a)
exp_a = np.exp(a - c) # 오버플로 대책
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
소프트맥스 함수의 특징
- 소프트맥스 함수의 출력은 0에서 1.0 사이의 실수
- 출력의 총합은 1
- 이 성질 덕분에 소프트맥스 함수의 출력을 ‘확률’로 해석할 수 있음
- 즉, 소프트맥스 함수를 이용함으로써 문제를 확률적(통계적)으로 대응할 수 있게 되는 것
- 주의점 : 소프트맥스 함수를 적용해도 각 원소의 대소 관계는 변하지 않음
- 지수 함수가 단조 증가함수이기 때문
- 신경망을 이용한 분류에서는 일반적으로 가장 큰 출력을 내는 뉴런에 해당하는 클래스로만 인식,
- 그리고 소프트맥스 함수를 적용해도 출력이 가장 큰 뉴런의 위치는 달라지지 않습니다.
- 결과적으로 신경망으로 분류할 때는 출력층의 소프트맥스 함수를 생략해도 됩니다.
- 현업에서도 지수 함수 계산에 드는 자원 낭비를 줄이고자 출력층의 소프트맥스 함수를 생략하는 것이 일반적입니다.
출력층의 뉴런 수 정하기
출력층의 뉴런 수는 풀려는 문제에 맞게 적절히 정해야 합니다.
- 분류에서는 분류하고 싶은 클래스 수로 설정하는 것이 일반적
- 예시) 입력 이미지를 숫자 0부터 9 중 하나로 분류하는 문제라면 출력층의 뉴런을 10개로 설정
Reference
본 글은 밑바닥부터 시작하는 딥러닝을 참고하여 작성하였습니다.
'Data Science > Deep Learning' 카테고리의 다른 글
| [DL] 오차역전파법(Backpropagation) (2) | 2022.03.08 |
|---|---|
| [DL] 신경망 학습 (0) | 2022.03.04 |
| [DL] 손실함수 (Loss Function) : 오차제곱합(SSE), 교차 엔트로피 오차(Cross-Entropy) (0) | 2022.03.04 |
| [DL] 신경망 활성화 함수 - 시그모이드(sigmoid), ReLU, 계단함수 (0) | 2022.02.25 |
| [DL] 퍼셉트론(Perceptron) (0) | 2022.02.24 |




댓글